Chapter 10 Causality and Matching
Causality is a concept that statisticians and statistical science traditionally shy away from. Recently, however, many successful attempts have been made to include the concept of causality in the statistical theory and vocabulary. A good review of the topic, from a modern, event history analysis point of view, is given in Aalen, Borgan, and Gjessing (2008), Chapter 9. Some of their interesting ideas are presented here.
The traditional standpoint among statisticians was that “we deal with association and correlation, not causality,” see Pearl (2000) for a discussion. An exception was the clinical trial, and other situations, where randomization could be used as a tool. However, during the last couple of decades, there has been an increasing interest in the possibility to make causal statements even without randomization, that is, in observational studies (Rubin 1974; Robins 1986).
Matching is statistical technique, which has an old history without an explicit connection to causality. However, as we will see, matching is a very important tool in the modern treatment of causality.
10.1 Philosophical Aspects on Causality
The concept of causality has a long history in philosophy, see for instance Aalen, Borgan, and Gjessing (2008) for a concise review. A fundamental question, with a possibly unexpected answer, is “Does everything that happens have a cause?” According to Zeilinger (2005), the answer is “No.”
“The discovery that individual events are irreducibly random is probably one of the most significant findings of the twentieth century. Before this, one could find comfort in the assumption that random events only seem random because of our ignorance … But for the individual event in quantum physics, not only do we not know the cause, there is no cause.”
Of course, this statement must not necessarily be taken literally, but it indicates that nothing is to be taken as granted.
10.2 Causal Inference
According to Aalen, Borgan, and Gjessing (2008), there are three major schools in statistical causality, (i) graphical models, (ii) predictive causality, and (iii) counterfactual causality. They also introduce a new concept, dynamic path analysis, which can be seen as a merging of (i) and (ii), with the addition that time is explicitly entering the models.
10.2.1 Graphical models
Graphical models have a long history, emanating from Wright (1921) who introduced path analysis. The idea was to show by writing diagrams how variables influence one another. Graphical models has had a revival during the last decades with very active research, see Pearl (2000) and Lauritzen (1996). A major drawback, for event history analysis purposes, is, according to Aalen, Borgan, and Gjessing (2008), that time is not explicitly taken into account. Their idea is that causality evolves in time, that is, a cause must precede an effect.
10.2.2 Predictive causality
The concept of predictive causality is based on stochastic processes, and that a cause must precede an effect in time. This may seem obvious, but very often you do not see it clearly stated. This leads sometimes to confusion, for instance to questions like “What is the cause, and what is the effect?”
One early example is Granger causality (Granger 1969) in time series analysis. Another early example with more relevance in event history analysis is the concept of local dependence. It was introduced by Tore Schweder (Schweder 1970).
Local dependency is exemplified in Figure 10.1.
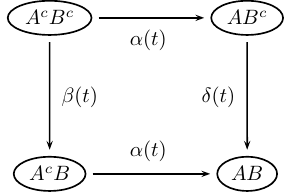
FIGURE 10.1: Local dependence.
Here \(A\) and \(B\) are events, and the superscript (\(c\)) indicates their complements, i.e., they have not (yet) occurred if superscripted. This model is used in the matched data example concerning infant and maternal mortality in a 19th century environment later in this chapter. There \(A\) stands for mother dead and \(B\) means infant dead. The mother and her new-born (alive) infant is followed from the birth to the death of the infant (but at most a one-year follow-up). During this follow-up both mother and infant are observed and the eventual death of the mother is reported. The question is whether mother’s death influences the survival chances of the infant (it does!).
In Figure 10.1: If \(\beta(t) \ne \delta(t)\), then \(B\) is locally dependent on \(A\), but \(A\) is locally independent on \(B\): The vertical transition intensities are different, which means that the intensity of \(B\) happening is influenced by \(A\) happening or not. On the other hand, the horizontal transitions are equal, meaning that the intensity of \(A\) happening is not influenced by \(B\) happening or not. In our example this means that mother’s death influences the survival chances of the infant, but mother’s survival chances are unaffected by the eventual death of her infant (maybe not probable in the real world).
10.2.3 Counterfactuals
In situations, where interest lies in estimating a treatment effect (in a wide sense), the idea of counterfactual outcomes is an essential ingredient in the causal inference theory advocated by Rubin (1974) and Robins (1986). A good introduction to the field is given by Hernán and Robins (2020).
Suppose we have a sample of individuals, some treated and some not treated, and we wish to estimate a marginal (in contrast to conditional) treatment effect in the sample at hand. If the sample is the result of randomization, that is, individuals are randomly allocated to treatment or not treatment (placebo), then there are in principle no problems. If, on the other hand, the sample is self-allocated to treatment or placebo (an observational study), then the risk of confounders destroying the analysis is overwhelming. A confounder is a variable that is correlated both with treatment and effect, eventually causing biased effect estimates.
The theory of counterfactuals tries to solve this dilemma by allowing each individual to be its own control. More precisely, for each individual, two hypothetical outcomes are defined; the outcome if treated and the outcome if not treated. Let us call them \(Y_1\) and \(Y_0\), respectively. They are counterfactual (counter to fact), because none of them can be observed. However, since an individual cannot be both treated and untreated, in the real data, each individual has exactly one observed outcome \(Y\). If the individual was treated, then \(Y = Y_0\), otherwise \(Y = Y_1\). The individual treatment effect is \(Y_1 - Y_0\), but this quantity is not possible to observe, so how to proceed?
The Rubin school fixes balance in the data by matching, while the Robins school advocates inverse probability weighting. Both these methods are possible to apply to event history research problems (Hernán, Brumback, and Robins 2002; Hernán et al. 2005), but unfortunately there is few, if any, publicly available R packages for performing these kinds of analyzes, partly with the exception of matching, of which an example is given later in this chapter. However, with the programming power of R, it is fairly straightforward to write own functions for specific problems. This is however out of the scope of this presentation.
The whole theory based on counterfactuals relies on the assumption that there are no unmeasured confounders. Unfortunately, this assumption is completely un-testable, and even worse, it never holds in practice.
10.3 Aalen’s Additive Hazards Model
In certain applications it may be reasonable to assume that risk factors acts additively rather than multiplicatively on hazards. Aalen’s additive hazards model (Aalen 1989, 1993) takes care of that.
For comparison, recall that the proportional hazards model may be written \[\begin{equation*} h(t\mid \mathbf{x_i}) = h_0(t) r\bigl(\boldsymbol{\beta}, \mathbf{x_i(t)}\bigr), \quad t > 0, \end{equation*}\] where \(r(\boldsymbol{\beta}, \mathbf{x_i})\) is a relative risk function. In Cox regression we (usually) have: \(r(\boldsymbol{\beta}, \mathbf{x_i}) = \exp(\boldsymbol{\beta}^T \mathbf{x_i})\),
The additive hazards model is given by \[\begin{equation*} h(t \mid \mathbf{x_i}) = h_0(t) + \beta_1(t) x_{i1}(t) + \cdots +\beta_p(t) x_{ip}(t), \quad t > 0, \end{equation*}\] where \(h_0(t)\) is the baseline hazard function, and \({\boldsymbol{\beta}(t)} = (\beta_0(t), \ldots, \beta_p(t))\) is a (multivariate) nonparametric regression function.
Note that \(h(t, \mathbf{x_i})\) may be negative, if some coefficients or variabless are negative. In contrast to the Cox regression model, there is no automatic protection against this.
The function aareg in the survival package fits the additive model.
Call:
survival::aareg(formula = Surv(enter - 60, exit - 60, event) ~
sex, data = oldmort)
n= 6495
1805 out of 1806 unique event times used
slope coef se(coef) z p
Intercept 0.1400 0.000753 2.58e-05 29.20 9.82e-188
sexfemale -0.0281 -0.000136 3.26e-05 -4.16 3.12e-05
Chisq=17.34 on 1 df, p=3.12e-05; test weights=aalenObviously sex is an important variable, females have lower mortality than men.
Plots of the time-varying intercept and regression coefficient are given by
oldpar <- par(mfrow = c(1, 2))
plot(fit)
par(oldpar)See Figure 10.2, where 95% confidence limits are added around
the fitted time-varying coefficients. Also note the use of the function
par; the first call sets the plotting area
to “one row and two columns” and saves the old par setting in
oldpar. Then the plotting area is restored to what it was earlier. It is a
good habit to always clean up for the next plotting enterprise.
FIGURE 10.2: Cumulative intercept (left) and cumulative regression coefficient (right).
10.4 Dynamic Path Analysis
The term dynamic path analysis was coined by Odd Aalen and coworkers (Aalen, Borgan, and Gjessing 2008). It is an extension, by explicitly introducing time, of path analysis described by Wright (1921).
The inclusion of time in the model implies that there are one path analysis at each time point, see Figure 10.3.
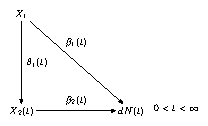
FIGURE 10.3: Dynamic path analysis.
\(X_2\) is an intermediate covariate, while \(X_1\) is measured at baseline (\(t =0\)). \(dN(t)\) is the number of events at \(t\).
The structural equations \[\begin{equation*} \begin{split} dN(t) &= \bigl(\beta_0(t) + \beta_1(t) X_1 + \beta_2(t) X_2(t)\bigr)dt + dM(t) \\ X_2(t) &= \theta_0(t) + \theta_1(t) X_1 + \epsilon(t) \end{split} \end{equation*}\] are estimated by ordinary least squares (linear regression) at each \(t\) with \(dN(t) > 0\).
Then the second equation is inserted in the first:
\[\begin{multline*} dN(t) = \bigl\{\beta_0(t) + \beta_2(t) \theta_0(t) + \\ \bigl(\beta_1(t) + \theta_1(t) \beta_2(t)\bigr) X_1 + \beta_2(t) \epsilon(t)\bigr\}dt + dM(t) \end{multline*}\]
and the total treatment effect is \(\bigl(\beta_1(t) + \theta_1(t)\beta_2(t)\bigr)dt\), so it can be split into two parts according to
\[\begin{equation*}
\begin{split}
\text{total effect} &= \text{direct effect} + \text{
indirect effect} \\
&= \beta_1(t)dt + \theta_1(t)\beta_2(t)dt
\end{split}
\end{equation*}\]
Some book-keeping is necessary in order to write an R function for this
dynamic model. Of great help is the function
risksets in eha;
it keeps track of the composition of the riskset over time, which is
exactly what is needed for implementing the dynamic path analysis. For application
where dynamic path analysis is used, see Broström and Bengtsson (2011).
Estimation: Standard least squares at each \(t, \; 0 < t < \infty\) (in principle).
10.5 Matching
Matching is a way of eliminating the effect of confounders and therefore important to discuss in connection with causality. One reason for matching is the wish to follow the causal inference paradigm with counterfactuals. Another reason is that the exposure we want to study is very rare in the population. It will then be inefficient to take a simple random sample from the population; in order to get enough cases in the sample, the sample size needs to be very large. On the other hand, today’s register based research tends to analyze whole populations, and the limitations in terms of computer memory and process power are more or less gone. Nevertheless, small properly matched data sets may contain more information about the specific question at hand than whole register!
When creating a matched data set, you have to decide how many controls you want per case. In the true counterfactual paradigm in “causal inference,” it is common practice to choose one control per case, to “fill in” the unobservable in the pair of counterfactuals. We first look at the case with matched pairs, then a case study with two controls per case.
10.5.1 Paired data
Certain kinds of observations come naturally in pairs. The most obvious situation is data from twin studies. Many countries keep registers of twins, and the obvious advantage with twin data is that it is possible to control for genetic variation; monozygotic twins have identical genes. Humans have pairs of many body parts; arms, legs, eyes, ears, etc. This can be utilized in medical studies concerning comparison of treatments, the two in a pair simply get one treatment each.
In a survival analysis context, pairs are followed over time and it is noted who first experience the event of interest. In each pair, one is treated and the other is a control, but otherwise they are considered more or less identical. Right censoring may result in that it is impossible to decide who in the pair experienced the event first. Such pairs are simply discarded in the analysis.
The model is \[\begin{equation} h_i(t; x) = h_{0i}(t) e^{\beta x}, \end{equation}\] where \(x\) is treatment (0–1) and \(i\) is pair No. Note that each pair has its own baseline hazard function, which means that the proportional hazards assumption is only required within pairs. This is a special form of stratified analysis in that each stratum only contains two individuals, a case and its control. If we denote by \(T_{i1}\) the life length of the case in pair No. i and \(T_{i0}\) the life length of the corresponding control, we get
\[\begin{equation} P(T_{1i} < T_{0i}) = \frac{e^\beta}{1 + e^\beta}, \quad i = 1, \ldots, n, \tag{10.1} \end{equation}\] and the result of the analysis is simply a study of binomial data; how many times did the case die before the control? We can estimate this probability, and also test the null hypothesis that it is equal to one half, which corresponds to \(\beta = 0\) in equation (10.1).
10.5.2 More than one control
The situation with more than one control per case is as simple as the paired data case to handle. Simply stratify, with one case and its controls per stratum. It is also possible to have a varying number of controls per case.
As an example where two controls per case were used, let us see how a study of maternal death and its effect on infant mortality was performed.
This is a study on historical data from northern Sweden, 1820–1895 (Broström 1987). The simple question asked was: How much does the death risk increase for an infant that loses her mother? More precisely, by a maternal death we mean that a mother dies within one year after the birth of her child. In this particular study, only first births were studied. The total number of such births was 5641 and of these 35 resulted in a maternal death (with the infant still alive). Instead of analyzing the full data set, it was decided to use matching. To each case of maternal death, two controls were selected in the following way. At each time an infant changed status from mother alive to mother dead, two controls are selected without replacement from the subset of the current risk set, where all infants have mother alive and not already used as controls and with correct matching characteristics. If a control changes status to case (its mother dies), it is immediately censored as a control and starts as a case with two controls linked to it. However, this situation never occurred in the study. Let us load the data into R and look at it, see Table ??.
Here we see the two first triplets in the data set, which consists of 35
triplets, or 105 individuals. Infant No. 1 (the first row) is a case, his
mother died when he was 55 days old. At that moment, two controls were
selected, that is, two boys 55 days of age, and with the same characteristics
as the case. The matching was not completely successful; we had to look a
few years back and forth in calendar time (covariate year). Note also
that in this triplet all infants survived one year of age, so there is no
information of risk differences in that triplet. It will be automatically
removed in the analysis.
The second triplet, on the other hand, will be used, because the case dies at age 76 days, while both controls survive one year of age. This is information suggesting that cases have higher mortality than controls after the fatal event of a maternal death.
The matched data analysis is performed by stratifying on triplets (the
variable stratum), see Table 10.1.
| Covariate | level | W_mean | Coef | HR | SE | LR_p |
|---|---|---|---|---|---|---|
| mother | 0.0000 | |||||
| alive | 0.763 | 0 | 1 | |||
| dead | 0.237 | 2.6052 | 13.5344 | 0.7567 | ||
| Max Log | Likelihood | -10.8 |
The result is that mother’s death increases the death risk of the infant wit a factor 13.5! It statistically very significant, but the number of infant deaths (21) is very small, so the \(p\)-value may be unreliable.
In a stratified analysis it is normally not possible to include covariates that are constant within strata. However, here it is possible to estimate the interaction between a stratum-constant covariate and exposure, mother’s death. However, it is important not to include the main effect corresponding to the stratum-constant covariate! This is a rare exception to the rule that when an interaction term is present, the corresponding main effects must be included in the model.
We investigate whether the effect of mother’s death is modified by her age
by first calculating an interaction term (mage):
infants$mage <- ifelse(infants$mother == "dead", infants$age, 0) Note the use of the function ifelse:
It takes three arguments, the first is a logical expression resulting in
a logical vector, with values TRUE and FALSE. Note that
in this example, the length is the same as the length of mother (in
infants). For each component that is TRUE, the result is given by
the second argument, and for each component that is FALSE the value
is given by the third argument.
| Covariate | level | W_mean | Coef | HR | SE | LR_p |
|---|---|---|---|---|---|---|
| mother | 0.5618 | |||||
| alive | 0.763 | 0 | 1 | |||
| dead | 0.237 | 2.9160 | 18.4670 | 4.8598 | ||
| mage | 6.684 | -0.0122 | 0.9878 | 0.1884 | 0.9485 | |
| Max Log | Likelihood | -10.8 |
What happened here? The effect of mother’s age is even larger than in the
case without mage, but the statistical significance is gone
altogether. There are two problems with one solution here. First, due to the
inclusion of the interaction, the (main) effect of mother’s death is now
measured at mother’s age equal to 0 (zero!), which of course is completely
nonsensical, and second, the construction makes the two covariates strongly
correlated: When mother is alive, mage is zero, and
when mother is dead, mage takes a rather large
value. This is a case of collinearity, however
not very severe case, because it is very easy to get rid of.
The solution? Center mother’s age (age)! Recreate the
variables and run the analysis again:
infants$age <- infants$age - mean(infants$age)
infants$mage <- ifelse(infants$mother == "dead", infants$age, 0)The result is in Table 10.3.
| Covariate | level | W_mean | Coef | HR | SE | LR_p |
|---|---|---|---|---|---|---|
| mother | 0.0000 | |||||
| alive | 0.763 | 0 | 1 | |||
| dead | 0.237 | 2.5858 | 13.2739 | 0.8089 | ||
| mage | 0.280 | -0.0122 | 0.9878 | 0.1884 | 0.9485 | |
| Max Log | Likelihood | -10.8 |
The two fits are equivalent (look at the Max. log. likelihoods), but with different parameterizations. The second, with a centered mother’s age, is preferred, because the two covariates are close to uncorrelated there.
A subject-matter conclusion in any case is that mother’s age does not affect the effect of her death on the survival chances of her infant.
A general advice: Always center continuous covariates before the analysis! This is especially important in the presence of models with interaction terms, and the advice is valid for all kinds of regression analyzes, not only Cox regression. Common practice is to subtract the mean value, but it is usually a better idea to use a fixed value, a value that remains fixed as subsets of the original data set are analyzed.
10.6 Conclusion
Finally some thoughts about causality, and the techniques in use for “causal inference.” As mentioned above, in order to claim causality, one must show (or assume) that there are “no unmeasured confounders.” Unfortunately, this is impossible to prove or show from data alone, but even worse is the fact that in practice, at least in demographic and epidemiological applications, there are always unmeasured confounders present. However, with this in mind, note that
- Causal thinking is important,
- Counterfactual reasoning and marginal models yield little insight into
“how it works,” but it is a way of reasoning around research problems
that helps sorting out thoughts.
- Joint modeling is the alternative.
- Creation of pseudo-populations
through weighting and matching may limit the understanding of
how things really work.
- Analyze the process as it presents itself, so that it is easier to generalize findings.
Read more about this in Aalen, Borgan, and Gjessing (2008).